
안녕하세요, 여러분! 오늘은 “회로이론 – 라플라스 변환표” 에 대해 이야기해보려 합니다. 전자공학을 공부하거나 관련된 일을 하시는 분들께는 정말 유용한 정보가 될 거예요. 저는 예전에 이 부분을 공부하면서 많은 어려움을 겪었는데, 오늘은 제가 직접 정리한 내용을 통해 여러분께 조금이라도 도움이 되었으면 좋겠어요.
회로 이론은 전기 전자 공학에서 매우 중요한 분야인데요. 그 중에서도 라플라스 변환은 회로 분석을 쉽게 할 수 있게 해줍니다. 최근에 대학에 입학한 저도 처음에는 라플라스 변환이 어렵게 느껴졌는데요. 하지만 차근차근 공부하다 보니 생각보다 이해하기 쉽더라고요. 오늘은 라플라스 변환표를 살펴보면서 회로 이론의 핵심 개념을 정리해보려 합니다.
라플라스 변환이란? – 회로이론 필수 개념
라플라스 변환은 미분 방정식으로 표현된 회로 문제를 대수 방정식으로 변환시켜 해결할 수 있게 해줍니다. 시간 영역의 신호를 복소수 평면 상의 주파수 영역으로 변환시키는 수학적 기법이라고 할 수 있죠. 이를 통해 회로 분석이 훨씬 수월해집니다.
라플라스 변환의 기본 개념
라플라스 변환은 다음과 같은 수식으로 정의돼요: $$ F(s) = \int_{0}^{\infty} f(t)e^{-st} dt $$ 여기서 ( f(t) )는 시간 영역의 함수이고, ( F(s) )는 복소수 영역의 함수입니다. ( s )는 복소수이며, 일반적으로 ( s = \sigma + j\omega )로 표현돼요.
공대 수학의 꽃, 라플라스 변환표라플라스 변환표 – 필수 공식들
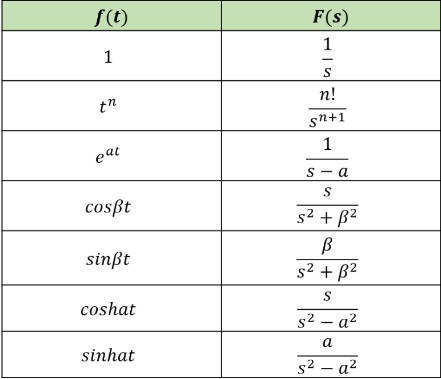
라플라스 변환표를 통해 자주 사용되는 함수들의 변환 결과를 쉽게 찾을 수 있어요. 아래에 몇 가지 중요하고 자주 사용되는 라플라스 변환 공식들을 정리해볼게요.
[ 회로이론 ]전기에서 자주나오는 라플라스 변환 표1. 단위 계단 함수 (Unit Step Function)
단위 계단 함수 ( u(t) )의 라플라스 변환은 다음과 같아요: $$ u(t) \rightarrow \frac{1}{s} $$ 이 공식은 회로에서 스위치가 켜지는 순간을 표현할 때 유용해요.
2. 지수 함수 (Exponential Function)
지수 함수 ( e^{at} )의 라플라스 변환은 다음과 같아요: $$ e^{at} \rightarrow \frac{1}{s-a} $$ 이를 통해 시간 도메인의 지수 증가나 감소를 주파수 도메인에서 쉽게 표현할 수 있어요.
3. 삼각 함수 (Trigonometric Function)
삼각 함수의 경우, 사인 함수와 코사인 함수의 라플라스 변환은 다음과 같아요: $$ \sin(at) \rightarrow \frac{a}{s^2 + a^2} $$ $$ \cos(at) \rightarrow \frac{s}{s^2 + a^2} $$ 이 공식들은 주파수 응답 분석에서 매우 유용해요.
라플라스 변환 – 변환표라플라스 변환표 활용법 – 실전 예제
예제 1: RC 회로의 응답 분석
간단한 RC 회로에서 커패시터 전압을 분석할 때, 라플라스 변환을 사용하면 미분 방정식을 쉽게 풀 수 있어요. 예를 들어, 회로의 입력이 단위 계단 함수라면, 출력 전압은 다음과 같이 구할 수 있어요: $$ V_{out}(s) = \frac{1}{s(RC + 1)} $$ 이를 다시 시간 영역으로 변환하면: $$ V_{out}(t) = 1 – e^{-\frac{t}{RC}} $$ 이렇게 간단히 회로의 응답을 구할 수 있어요.
예제 2: RLC 회로의 주파수 응답
RLC 회로의 경우, 입력이 사인파일 때의 출력 응답을 라플라스 변환을 통해 분석할 수 있어요. 예를 들어, 입력이 ( \sin(\omega t) )일 때, 출력은 다음과 같이 구할 수 있어요: $$ V_{out}(s) = \frac{\omega}{(s^2 + \omega^2)(s^2 + s\frac{R}{L} + \frac{1}{LC})} $$ 이를 통해 주파수 응답을 쉽게 분석할 수 있어요.
후기 및 경험 사례
이처럼 라플라스 변환표를 잘 활용하면 복잡한 회로 문제도 쉽게 해결할 수 있습니다. 물론 처음에는 익숙하지 않겠지만, 꾸준히 연습하다 보면 회로 이론 문제를 능숙하게 풀 수 있게 될 거예요.
마무리
오늘 라플라스 변환표를 살펴보며 회로 이론의 핵심 개념을 정리해보았습니다. 처음에는 어려워 보였지만, 차근차근 공부하다 보니 생각보다 이해하기 쉽더라고요. 앞으로도 꾸준히 연습하면서 회로 이론 실력을 키워나가겠습니다. 여러분도 이 글을 통해 회로 이론에 대한 이해도가 높아지셨으면 좋겠습니다. 감사합니다!
다음 시간에는 더 유익한 정보로 찾아뵐게요. 감사합니다!






